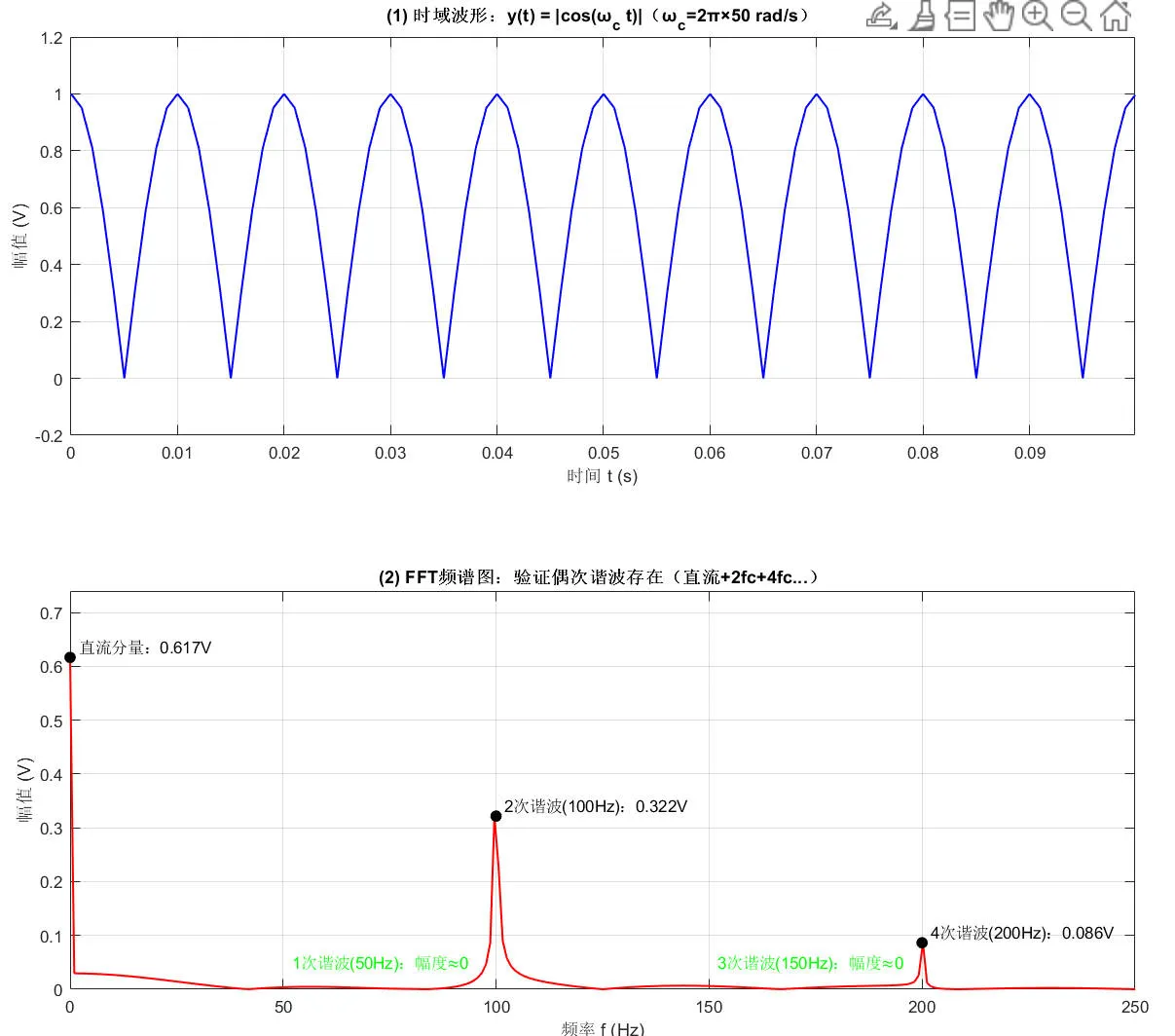
• 常规 AM（DSB-AM）——常规双边带幅度调制
• DSB（DSB-SC）——抑制载波的双边带调制

ma调制指数计算

常规调幅（DSB-AM，双边带全载波调幅）是唯一具有传统意义上调制指数 $m_a$​ 的调幅方式。

该参数是衡量调幅深度和失真风险的关键指标。调制指数 $m_a$ 衡量的是已调波包络的最大变化程度。在常规 AM 中，已调波的包络电压 $V_{\text{包络}}(t)$ 是由直流偏置 $V_c$ 和调制信号 $V_{cm}\cos(\Omega t)$ 共同决定的：

$V_{\text{包络}}(t) = V_c + V_{cm}\cos(\Omega t) = V_c \left(1 + m_a\cos(\Omega t)\right)$

调制指数 $m_a$ 的定义与公式

调制指数 $m_a$ 定义为调制信号最大振幅 $V_{cm}$ 与载波静态幅度 $V_c$（或称直流偏置）的比值。

• 公式：

  $m_a = \frac{V_{cm}}{V_c}$

• 参数说明：

  • $V_{cm}$：调制信号（如低频正弦信号）的最大振幅（峰值）。
  • $V_c$：载波的静态幅度（即未调制时的载波峰值，由直流偏置决定）。

• 取值限制：

  调制指数 $m_a$ 的取值范围必须满足：

  $0 \le m_a \le 1$

  当 $m_a > 1$ 时，信号将发生过调制失真（包络检波器无法正确还原调制信号）。

$m_a$ 与直流偏置 $V_c$ 的关系计算

根据 $m_a$ 的定义公式，在已知调制信号振幅 $V_{cm}$ 和目标调制指数 $m_a$ 的情况下，可以直接计算出所需的直流偏置 $V_c$。

已知条件：

• 调制信号振幅 $V_{cm} = 1\text{V}$
• 目标调制指数 $m_a$（待定）

公式推导：

由 $m_a = \frac{V_{cm}}{V_c}$ 可得：

$V_c = \frac{V_{cm}}{m_a}$

具体计算示例：

基于乘法器的 AM 调制实现与 $m_a$ 的关系

在实际的调制电路中，常采用加偏置后与载波相乘的方式实现常规 AM 调制。

调制过程的数学表示

1. 调制信号加偏置：

   原始调制信号为 $m(t) = V_{cm}\cos(\Omega t)$。

   加入直流偏置 $V_b$ 后，输入乘法器的信号为：

   $v_{in}(t) = V_b + V_{cm}\cos(\Omega t)$

2. 与载波相乘：

   无偏置载波为 $c(t) = A_c\cos(\omega_c t)$。

   最终的已调波 $s(t)$ 为两者相乘：

   $s(t) = c(t) \cdot v_{in}(t) = A_c \left(V_b + V_{cm}\cos(\Omega t)\right) \cos(\omega_c t)$

与常规 AM 标准式的对应

常规 AM 的标准时域表达式为：

$s(t) = V_c \left(1 + m_a\cos(\Omega t)\right) \cos(\omega_c t)$

将乘法器得到的 $s(t)$ 表达式展开：

$s(t) = (A_c V_b) \cdot \left(1 + \frac{V_{cm}}{V_b}\cos(\Omega t)\right) \cdot \cos(\omega_c t)$

通过对比，可以得出如下等价关系：

1. 常规 AM 的 “载波静态幅度” $V_c$：

   $V_c = A_c \cdot V_b$

   $V_c$ 是载波振幅 $A_c$ 和偏置电压 $V_b$ 的乘积。

2. 调制指数 $m_a$：

   $m_a = \frac{V_{cm}}{V_b}$

   核心结论： 调制指数 $m_a$ 仅由调制信号振幅 $V_{cm}$ 和所加的偏置 $V_b$ 决定，与载波振幅 $A_c$ 没有直接关系。只要 $V_b$ 固定，不管 $A_c$ 怎么变化，$m_a$ 都不变。

载波振幅 $A_c$ 的实际工程限制

虽然 $A_c$ 不影响 $m_a$ 的计算值，但在实际系统中 $A_c$ 不能任意选取，必须考虑以下工程因素：

• 功率限制： $A_c$ 越大，已调波 $s(t)$ 的总功率越大。必须保证总功率不超过发射设备的功率上限。
• 信噪比 (SNR) 要求： $A_c$ 不能太小，否则已调波幅度过弱，在接收端解调时容易被噪声淹没，影响通信质量。
• 设备适配与失真： $A_c$ 需匹配后续放大、滤波等电路的线性输入范围。如果 $A_c$ 过大，会导致信号在电路中被“截断”，产生削波失真。

三种调制状态的定义

欠调制（Under-modulation）

• 条件： $0 \le m_a < 1$

• 物理表现： 调制信号的最大幅度 $V_{cm}$ 小于直流偏置 $V_c$。

  $V_{cm} < V_c$

• 结果： 在 $m_a = 0.5$ 的例子中，$V_{cm} = 1\text{V}$，而 $V_c = 2.0\text{V}$。

  此时，包络的最小幅度为：

  $V_{\text{包络, min}} = V_c - V_{cm} = 2.0\text{V} - 1.0\text{V} = 1.0\text{V}$

  包络在任何时刻都不会降到零或变为负值。这是无失真调制的理想状态，但效率较低。

临界调制（Critical Modulation 或 Full Modulation）

• 条件： $m_a = 1$

• 物理表现： 调制信号的最大幅度 $V_{cm}$ 等于直流偏置 $V_c$。

  $V_{cm} = V_c$

• 结果： 包络的最小幅度恰好为零：

  $V_{\text{包络, min}} = V_c - V_{cm} = 1.0\text{V} - 1.0\text{V} = 0\text{V}$

  这是最大无失真调制，功率效率最高。

过调制（Over-modulation）

• 条件： $m_a > 1$

• 物理表现： 调制信号的最大幅度 $V_{cm}$ 大于直流偏置 $V_c$。

  $V_{cm} > V_c$

• 结果： 包络的最小幅度将变为负值 ($V_{\text{包络, min}} < 0$)。

  这会导致信号的包络出现削波失真，无法通过常规的包络检波器正确解调出原始调制信号。

相干解调

仿真导入

这个是后期通信原理的一个基于Matlab的AM调制以及相干解调的仿真

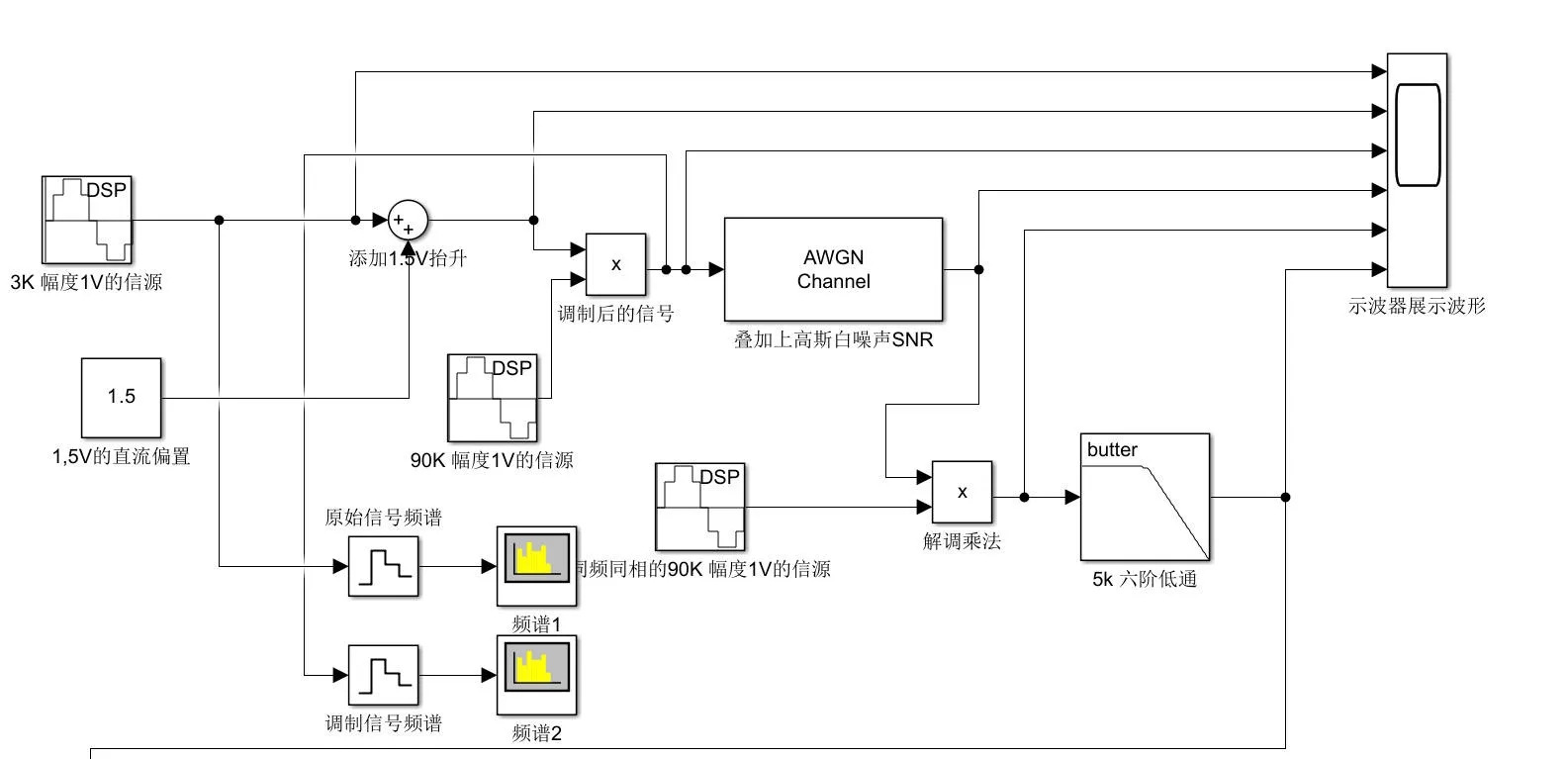
接下来我给出示波器所展示的波形的图片

第5行显示的波形，是相干解调后还没有经过低通滤波的原始波形

看见这张图片我们会产生一个疑问？ 为什么在相干解调前信号有正有负，但是相干解调后，所有的信号都在0以上？

这一块的原因其实是数学上的原因，具体如下：

为什么相干解调相乘后信号全在零轴以上？（数学本质）

AM信号的先天结构

调幅信号的表达式为：

其中 包络 $A + m(t) \geq 0$（调幅基本要求，避免“过调幅”失真），载波 $\cos(\omega_c t)$ 是正负交替的高频振荡（取值范围 $[-1, +1]$）。

相干解调的“相乘”操作

解调第一步，接收信号与同频同相的本地载波 $\cos(\omega_c t)$ 相乘：

$\cos^2(\omega_c t)$ 的非负性推导

核心是 平方运算的数学性质 + 三角恒等式：

• 取值范围分析：
  载波 $\cos(\omega_c t) \in [-1, +1]$，但平方后：

  $$\cos^2(\omega_c t) = \left[ \cos(\omega_c t) \right]^2 \geq 0$$

  即 $\cos^2(\omega_c t)$ 始终非负（取值范围 $[0, +1]$）。

• 三角恒等式验证：
  利用公式 $\cos^2(x) = \frac{1 + \cos(2x)}{2}$，令 $x = \omega_c t$，则：

  $$\cos^2(\omega_c t) = \frac{1}{2} + \frac{1}{2}\cos(2\omega_c t)$$

  由于 $\cos(2\omega_c t) \in [-1, +1]$，代入得：

  $$\frac{1}{2} + \frac{1}{2}\cos(2\omega_c t) \in \left[ \frac{1-1}{2}, \frac{1+1}{2} \right] = [0, +1]$$

  进一步证明 $\cos^2(\omega_c t)$ 恒非负。

最终波形的非负性

回到相乘结果 $s_{\text{product}}(t)$：

• 包络 $A + m(t) \geq 0$（调幅约束），
• 因子 $\cos^2(\omega_c t) \geq 0$（平方性质）。

两者非负相乘，故：

即 相乘后信号必然全在零轴上方。

相干解调中低通滤波还原基带信号的数学原理

滤波前的信号基础

相干解调第一步“相乘”后，得到的信号为：

结合三角恒等式 $\cos^2(\omega_c t) = \frac{1}{2} + \frac{1}{2}\cos(2\omega_c t)$，将上式展开分离高低频分量：

低通滤波的核心作用：分离高低频

信号分量的频率特性

• 低频分量：$\frac{A}{2} + \frac{1}{2}m(t)$
  其中 $m(t)$ 是基带信号（如语音、图像信号），其最高频率为 $f_m$（通常远小于载波频率 $f_c$，即 $f_m \ll f_c$），因此该分量的频率范围集中在 $[0, f_m]$。

• 高频分量：$\frac{A}{2}\cos(2\omega_c t) + \frac{1}{2}m(t)\cos(2\omega_c t)$

  • 第一项是 $2\omega_c$（即 $2f_c$）的纯倍频载波，频率固定为 $2f_c$；
  • 第二项是基带信号 $m(t)$ 对 $2\omega_c$ 载波的调幅，频率范围集中在 $[2f_c - f_m, 2f_c + f_m]$；
  • 核心特征：高频分量的最低频率 $2f_c - f_m \gg f_m$（因 $f_c \gg f_m$），与低频分量无重叠。

低通滤波器的参数选择

需选用 截止频率 $f_L$ 满足以下条件的低通滤波器（LPF）：

• 作用：允许低频分量 $\frac{A}{2} + \frac{1}{2}m(t)$ 完全通过，同时彻底抑制所有高频分量（$2f_c$ 附近的信号）。

滤波后的输出与基带信号还原

低通滤波的数学结果

经过低通滤波后，高频分量被完全滤除，仅保留低频分量，滤波器输出 $s_{\text{LPF}}(t)$ 为：

还原原始基带信号 $m(t)$

对滤波输出做简单线性变换，即可剥离直流分量 $\frac{A}{2}$，还原 $m(t)$：

数学本质总结

1. 相乘操作的核心是通过 $\cos^2(\omega_c t)$ 的恒等变换，将基带信号 $m(t)$ 从“载波调制态”（频率 $[f_c - f_m, f_c + f_m]$）转移到“低频态”（频率 $[0, f_m]$），同时产生可分离的倍频高频分量；
2. 低通滤波的本质是 利用频率分离特性，通过截止频率的合理选择，提取含基带信号的低频分量，滤除无用高频；
3. 最终通过线性变换剥离直流偏置，即可无失真还原原始基带信号 $m(t)$。

完整流程数学链

包络检波

AD8361 核心特性与包络检波原理

AD8361 是 真有效值（RMS）检波器，核心功能是将输入交流信号的幅度（RMS 值）转换为直流电压输出，适用于 射频（RF）调幅信号（AM）的包络提取。

1. 包络检波的数学逻辑（以 AM 信号为例）

AM 信号表达式：

• 包络：$A + m(t)$ 是基带信号（如语音），需从载波中提取。
• AD8361 的作用：测量 $s_{\text{AM}}(t)$ 的 RMS 值，利用 RMS 与包络的线性关系还原基带信号。

RMS 与包络的推导

计算 $s_{\text{AM}}(t)$ 的 RMS 值（有效值）：

AD8361 输出直流电压 $V_{\text{out}}$ 与 RMS 成正比：

其中 $K$​ 是芯片增益（可通过校准确定）。因此，$V_{\text{out}}$​ 直接反映包络 $A + m(t)$​ 的变化，实现包络检波。

二极管检波

二极管包络检波原理与核心公式

核心原理概述

二极管检波是 非相干解调 方案，利用二极管 单向导电性 实现信号整流，结合 RC低通滤波 提取AM信号包络，核心是“整流+滤波”的物理过程，无需本地载波，电路简单。

数学推导与关键公式

已知条件

• AM输入信号（包络非负，避免过调幅）：
  $s_{\text{AM}}(t) = \underbrace{[A + m(t)]}_{\text{非负包络}} \cdot \cos(\omega_c t)$
  其中：$A$=载波幅度，$m(t)$=基带信号（$|m(t)| \leq A$），$\omega_c = 2\pi f_c$=载波角频率，$f_c$=载波频率。

第一步：二极管整流（单向化处理）

理想二极管仅允许正半周信号通过，整流后输出：
$s_{\text{rec}}(t) = s_{\text{AM}}(t) \cdot u[s_{\text{AM}}(t)]$

• $u(\cdot)$=单位阶跃函数（$x>0$时$u(x)=1$，$x \leq 0$时$u(x)=0$）。
• 因$A + m(t) \geq 0$，简化为：
  $s_{\text{rec}}(t) = [A + m(t)] \cdot |\cos(\omega_c t)|$
  （$|\cos(\omega_c t)|$为单向高频载波，取值范围$[0,1]$​​）。

给 $u[s_{AM}(t)]$​ 下一个 “人话定义”它就是一个 “以 AM 信号为判断标准的全自动开关”：

AM虽然有包络，但是其本质就是无数高频信号相乘导致的一个外包络，并不是真实外围有一圈波

• 括号里的 (s_{AM}(t)) = 开关的 “判断依据”（看当前时刻的 AM 信号是正还是负）；

• 开关只有两个状态：0（关）和 1（开）；

• 判断规则：

  若当前 AM 信号 > 0（正电）→ 开关 = 1（开）；

  若当前 AM 信号 ≤ 0（负电或零）→ 开关 = 0（关）。

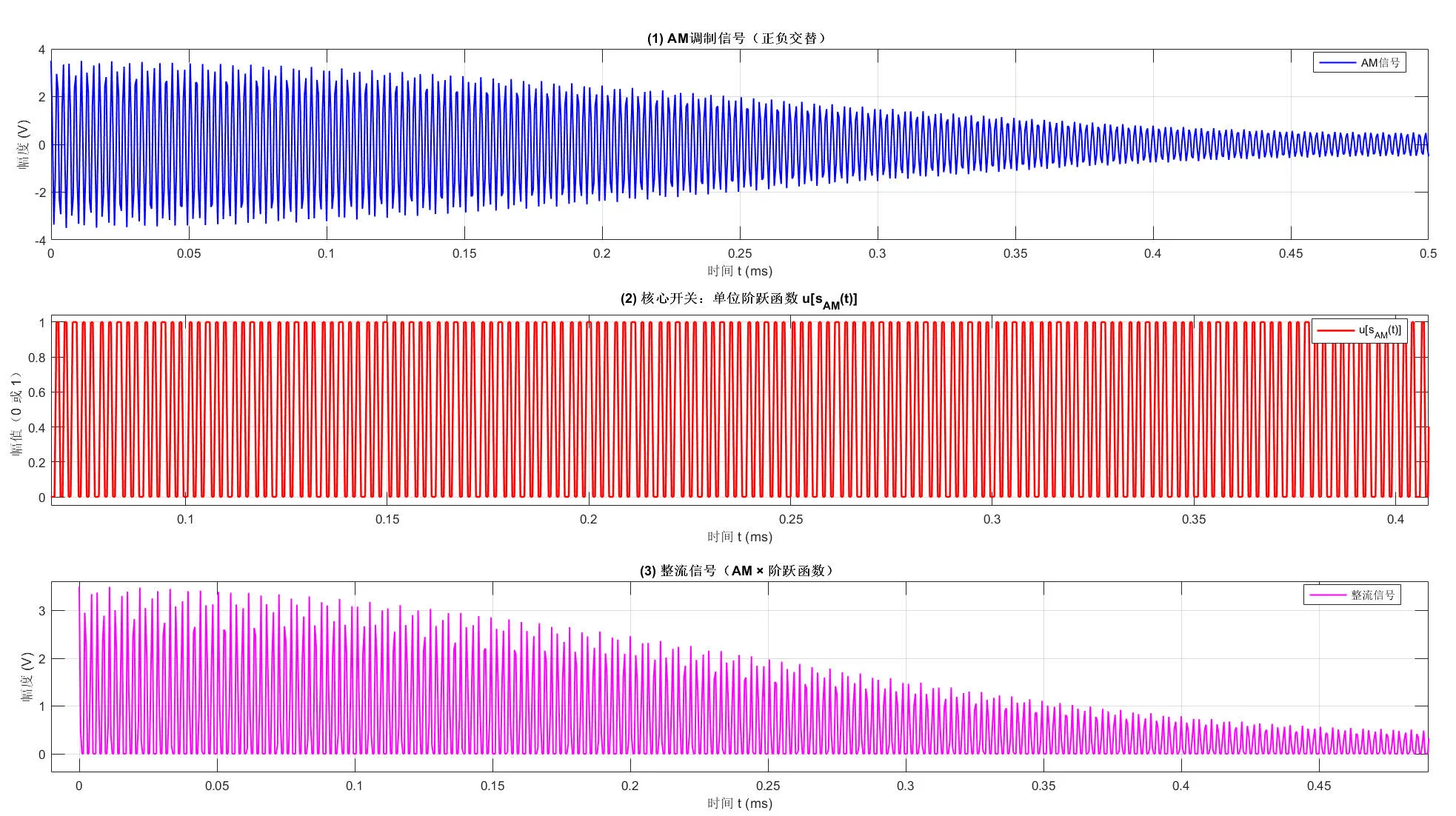
第二步：RC低通滤波（提取包络）

RC电路时间常数$\tau = R \cdot C$需满足 核心约束条件（无失真检波关键）：
$\frac{1}{\omega_c} \ll \tau \ll \frac{1}{\omega_m}$

• 展开为频率形式（更易工程应用）：
  $\frac{1}{2\pi f_c} \ll RC \ll \frac{1}{2\pi f_m}$
  其中：$\omega_m = 2\pi f_m$=基带信号最高角频率，$f_m$=基带信号最高频率（如语音$f_m \approx 3kHz$）。
• 物理意义：
  • $\tau \gg \frac{1}{2\pi f_c}$：电容充电快、放电慢，跟随载波峰值；
  • $\tau \ll \frac{1}{2\pi f_m}$：电容放电速度足够，跟随基带信号变化。

检波输出与基带信号还原

• RC滤波后输出（近似包络）：
  $v_o(t) \approx A + m(t)$
• 剥离直流分量，还原原始基带信号：
  $m(t) = v_o(t) - A$

核心公式汇总表

关键特点

1. 优点：电路极简（二极管+RC）、无需本地载波、成本低、功耗小；
2. 缺点：存在惰性失真（$\tau$​过大）、负峰切割失真（负载不匹配），动态范围较窄（30-40dB）。

包络为什么可以用低通滤波滤出

包络推导：从时域直观到数学逻辑

1. AM信号时域结构
   调制核心是“基带信号控制载波幅度”，原始AM信号：
   $s_{\text{AM}}(t) = E(t) \cdot \cos(\omega_c t) = [A + m(t)] \cdot \cos(\omega_c t)$
   其中 $f_c \gg f_m$（载波频率远大于基带频率，如 $f_c=455\text{kHz}$，$f_m=3\text{kHz}$）。
2. 瞬时幅度与包络提取
   任意时刻AM信号的瞬时幅度（绝对值）：
   $|s_{\text{AM}}(t)| = |A + m(t)| \cdot |\cos(\omega_c t)|$
   因 $A + m(t) \geq 0$，简化为 $[A + m(t)] \cdot |\cos(\omega_c t)|$。
   关键特性：$\cos(\omega_c t)$ 是高频振荡（周期 $T_c \ll T_m$），宏观上 $|\cos(\omega_c t)|$ 的振荡被“平均”，仅保留 $A + m(t)$ 的慢变趋势——即视觉上的“包络”

RC滤波近似推导：$s_{\text{LPF}}(t) \approx A + m(t)$

前提：整流后信号

二极管整流后，单向脉动信号含包络+高频载波：
$s_{\text{rec}}(t) = [A + m(t)] \cdot |\cos(\omega_c t)|$
$|\cos(\omega_c t)|$ 是周期 $T_c'=T_c/2$ 的非正弦信号，需通过 傅里叶级数分解 分离高低频。

步骤1：$|\cos(\omega_c t)|$ 傅里叶展开

分解为“直流+偶次谐波”（高次谐波幅度衰减可忽略）：
$|\cos(\omega_c t)| = \frac{2}{\pi} - \frac{4}{3\pi}\cos(2\omega_c t) + \frac{4}{15\pi}\cos(4\omega_c t) - ...$

核心分量：直流 $\frac{2}{\pi}$ + 高频谐波 $2\omega_c、4\omega_c...$

步骤2：代入整流信号，分离分量

步骤3：RC低通滤波（频域选通）

• 幅频特性：$f < f_L$（截止频率）通过，$f > f_L$ 衰减；
• 约束：$f_m < f_L < 2f_c - f_m$（确保高低频分离）；
• 输出：仅保留低频分量，高频被滤除：
  $s_{\text{LPF}}(t) = \frac{2}{\pi}[A + m(t)]$

步骤4：“约等于”的本质

$\frac{2}{\pi} \approx 0.636$ 是 常数增益，仅缩放幅度不改变信号形状，工程上可通过校准（乘以 $\frac{\pi}{2}$）还原，故简化为：
$s_{\text{LPF}}(t) \approx A + m(t) = E(t)$​

$|\cos(\omega_c t)|$与$\cos(\omega_c t)$​对比